[Python] 넘파이(Numpy)

넘파이

※ 라이브러리 사용법

import numpy 

A = numpy.array([1, 2])

print("A == ", A, ", type == ", type(A))

# 결과
A ==  [1 2] , type ==  <class 'numpy.ndarray'>

import numpy as np

A = np.array([1, 2])

print("A == ", A, ", type == ", type(A))

# 결과
A ==  [1 2] , type ==  <class 'numpy.ndarray'>

from numpy import exp

result = exp(1)

print("result == ", result, ", type == ", type(result))

# 결과
result ==  2.718281828459045 , type ==  <class 'numpy.float64'>

from numpy import *

result = exp(1) + log(1.7) + sqrt(2)

print("result == ", result, ", type == ", type(result))

# 결과
result ==  4.663123641894311 , type ==  <class 'numpy.float64'>

넘파이(Numpy)

vector / matrix 생성

• numpy는 머신러닝 코드 개발할 경우 자주 사용되는 벡터, 행렬 등을 표현하고 연산할 때 반드시 필요한 라이브러리
• 머신러닝에서는 숫자, 사람, 동물 등의 인식을 하기 위해서는 이미지(image) 데이터를 행렬(matrix)로 변환하는 것이 중요
• 행렬을 나타내기 위해서 리스트를 사용할 수도 있지만, 행렬 연산이 직관적이지 않고, 오류 가능성이 높기 때문에 행렬 연산을 위해서 numpy 사용이 필수!

# numpy vs list

import numpy as np

# list

A = [[1, 0], [0, 1]]
B = [[1, 1], [1, 1]]

print(A + B)

# numpy

A = np.array([[1, 0], [0, 1]])
B = np.array([[1, 1], [1, 1]])

print(A + B)

# 결과
[[1, 0], [0, 1], [1, 1], [1, 1]]
[[2 1]
 [1 2]]

 

• 머신러닝 코드 구현시, 연산을 위해서 vector, matrix 등의 형상(shape), 차원(dimension)을 확인하는 것이 필요!

A = np.array([1, 2, 3])
B = np.array([4, 5, 6])

# vector A, B 출력
print("A == ", A, ", B == ", B)

# vector A, B 형상 출력 => shape
print("A.shape == ", A.shape, ", B.shape == ", B.shape)

# vector A, B 차원 출력 => dimension
print("A.ndim == ", A.ndim, ", B.ndim == ", B.ndim)

# 결과
A ==  [1 2 3] , B ==  [4 5 6]
A.shape ==  (3,) , B.shape ==  (3,)
A.ndim ==  1 , B.ndim ==  1

 

• 벡터간 사칙연산(+, -, *, /)은 벡터의 각각의 원소에 대해서 수행됨

print("A + B == ", A + B)
print("A - B == ", A - B)
print("A * B == ", A * B)
print("A / B == ", A / B)

# 결과
A + B ==  [5 7 9]
A - B ==  [-3 -3 -3]
A * B ==  [ 4 10 18]
A / B ==  [0.25 0.4  0.5 ]

 

• 행렬은 벡터와 마찬가지로 np.array[[...], [...], [...])를 사용하여 생성
• reshape() 함수를 사용하여 벡터를 행렬로 변경하거나, 행렬을 다른 현상의 행렬로 변경할 수 있음

C = np.array([1, 2, 3])

# 벡터 형상 출력
print("C.shape == ", C.shape)

# 벡터를 1x3 행렬로 형 변환
C = C.reshape(1, 3)

# 행렬 형상 출력
print("C.shape == ", C.shape)

# 결과
C.shape ==  (3,)
C.shape ==  (1, 3)

행렬 곱 (dot product)

• A 행렬과 B 행렬의 곱 (dot product)는 np.dot(A, B) 으로 나타내며, 행렬 A의 열벡터와 행렬 B의 행벡터가 같아야 함
• 만약 같지 않다면, reshape() 또는 전치행렬(transpose) 등을 사용하여 형 변환을 한 후에 행렬 곱 실행

A = np.array([[1, 2, 3], [4, 5, 6]]) # 2x3 행렬
B = np.array([[-1, -2], [-3, -4], [-5, -6]]) # 3x2 행렬

# (2x3) dot product (3x2) = (2x2) 행렬
C = np.dot(A, B)

# matrix A, B 형상 출력 => shape
print("A.shape == ", A.shape, ", B.shape == ", B.shape)
print("C.shape == ", C.shape)
print(C)

# 결과
A.shape ==  (2, 3) , B.shape ==  (3, 2)
C.shape ==  (2, 2)
[[-22 -28]
 [-49 -64]]

 

• 행렬 곱은 행렬의 원소 개수가 같아야만 계산할 수 있는 사칙연산의 한계를 벗어남
• 행렬 곱 조건을 만족하는 다양한 크기의 행렬을 연속으로 만들고
• 행렬 곱을 연속으로 계산하면서
• 결과 값을 만들 수 있기 때문에 머신러닝과 이미지 프로세싱 분야에서 자주 사용됨
• 만약 행렬 곱을 사용하지 않으면, 똑같은 크기를 가지는 특성 값만을 사용해야 하기 때문에 다양한 특성을 갖는 필터 개발이 불가

전치행렬(transpose)

• 원본 행렬의 행은 열, 열은 행으로 바꾼 행렬
• 원본 행렬을 A라고하면 전치행렬은 A^T로 나타냄

A = np.array([[1, 2], [3, 4], [5, 6]]) # 3x2 행렬
B = A.T # A의 전치행렬 2x3

print("A.shape == ", A.shape, ", B.shape == ", B.shape)
print(A)
print(B)

# 결과
A.shape ==  (3, 2) , B.shape ==  (2, 3)
[[1 2]
 [3 4]
 [5 6]]
[[1 3 5]
 [2 4 6]]

# vector 전치행렬

C = np.array([1, 2, 3, 4, 5])
D = C.T # C가 vector이므로 transpose X

E = C.reshape(1, 5) # 1x5 matrix
F = E.T # E의 전치행렬 5x1

print("C.shape == ", C.shape, ", D.shape == ", D.shape)
print("E.shape == ", E.shape, ", F.shape == ", F.shape)
print(F)

# 결과
C.shape ==  (5,) , D.shape ==  (5,)
E.shape ==  (1, 5) , F.shape ==  (5, 1)
[[1]
 [2]
 [3]
 [4]
 [5]]

broadcast

• 행렬의 사칙연산은 기본적으로 두 개의 행렬의 크기가 같은 경우에만 수행이 가능
• 그러나 numpy에서는 크기가 다른 두 행렬 간의 사칙연산(+, -, *, /)을 할 수 있는데, 이를 브로드캐스트(broadcast) 라고 함
• 차원이 작은 쪽이 큰 쪽의 행 단위로 반복적으로 크기를 맞춘 후 계산

A = np.array([[1, 2], [3, 4]]) # [ [1, 2], [3, 4] ]
B = 5 # [ [5, 5], [5, 5] ]
C = np.array([4, 5]) # [ [4, 5] ]

print(A + B)
print(A + C)

# 결과
[[6 7]
 [8 9]]
[[5 7]
 [7 9]]

index / slice / iterator

• 행렬 원소를 명시적으로 접근하기 위해서는 리스트에서 처럼 index / slice 모두 사용 가능함

A = np.array([10, 20, 30, 40, 50, 60]).reshape(3, 2)

print("A.shape == ", A.shape)
print(A)

# 결과
A.shape ==  (3, 2)
[[10 20]
 [30 40]
 [50 60]]

print("A[0, 0] == ", A[0, 0], ", A[0, 1] == ", A[0, 1])
print("A[1, 0] == ", A[1, 0], ", A[1, 1] == ", A[1, 1])
print("A[2, 0] == ", A[2, 0], ", A[2, 1] == ", A[2, 1])

# 결과
A[0, 0] ==  10 , A[0, 1] ==  20
A[1, 0] ==  30 , A[1, 1] ==  40
A[2, 0] ==  50 , A[2, 1] ==  60

print("A[0:-1, 1:2] == ",A[0:-1, 1:2])

# 결과
A[0:-1, 1:2] ==  [[20]
 [40]]

print("A[ :, 0] == ", A[ :, 0])
print("A[ :, :] == ", A[ :, :])

# 결과
A[ :, 0] ==  [10 30 50]
A[ :, :] ==  [[10 20]
 [30 40]
 [50 60]]

 

• 명시적 index / slice 이외에, 행렬 모든 원소를 access 하는 경우에는 iterator 사용 가능
• numpy iterator는 next() 함수를 통해 데이터 값을 처음부터 끝까지 읽어 들이는 방법을 제공

A = np.array([[10, 20, 30, 40], [50, 60, 70, 80]])

print(A, "\n")
print("A.shape == ", A.shape, "\n")

# 행렬 A의 iterator 생성
# flags = ['multi_index'] : iterator 생성후 반복할때 행렬처럼 (row, column) 형태의 multi_index 형태로 동작
# op_flags = ['readwrite'] : iterator 를 R/W 형태로 생성
it = np.nditer(A, flags = ['multi_index'], op_flags = ['readwrite'])

while not it.finished:
    idx = it.multi_index
    print("current value => ", A[idx])
    it.iternext()

# 결과
[[10 20 30 40]
 [50 60 70 80]] 

A.shape ==  (2, 4) 

current value =>  10
current value =>  20
current value =>  30
current value =>  40
current value =>  50
current value =>  60
current value =>  70
current value =>  80

concatenate

• 행렬에 행(row) 또는 열(column)을 추가하기 위해 사용하는 함수
• 머신러닝의 회귀(regression) 코드 구현시 가중치(weight)와 바이어스(bias)를 별도로 구분하지 않고 하나의 행렬로 취급하기 위한 프로그래밍 구현 기술

# 행렬에 열과 행 추가

A = np.array([[10, 20, 30], [40, 50, 60]])

print(A.shape)

# A matrix에 행(row) 추가할 행렬, 1x3 reshape
# 행을 추가하기 때문에 우선 열을 3열로 만들어야 함
row_add = np.array([70, 80, 90]).reshape(1, 3)

# A matrix에 열(column) 추가할 행렬, 2x1 reshape
# 열을 추가하기 때문에 우선 행을 2행으로 만들어야 함
column_add = np.array([1000, 2000]).reshape(2, 1)

# numpy.concatenate 에서 axis = 0 (행 기준)
B = np.concatenate((A, row_add), axis = 0)

print(B)

# numpy.concatenate 에서 axis = 1 (열 기준)
C = np.concatenate((A, column_add), axis = 1)

print(C)

# 결과
(2, 3)
[[10 20 30]
 [40 50 60]
 [70 80 90]]
[[  10   20   30 1000]
 [  40   50   60 2000]]

useful functions (loadtxt(), rand(), argmax() ... )

loadtxt()

• seperator로 구분된 파일에서 데이터를 읽기 위해 사용하는 함수
• 리턴 값은 행렬이기 때문에 index / slice 이용하여 데이터를 분리할 수 있음
• 머신러닝 코드에서 입력 데이터와 정답 데이터를 분리하는 프로그래밍 기법

# 데이터는 25x4 행렬이라고 가정
loaded_data = np.loadtxt('./data-01.csv', delimiter = ',', dtype = np.float32)

x_data = loaded_data[ :, 0:-1] # 모든 행, 3열까지의 데이터
t_data = loaded_data[ :, [-1]] # 모든 행, 4열의 데이터

print("x_data.ndim == ", x_data.ndim, ", x_data.shape == ", x_data.shape)
print("t_data.ndim == ", t_data.ndim, ", t_data.shape == ", t_data.shape)

# 결과
# x_data.ndim == 2, x_data.shape == (25, 3)
# t_data.ndim == 2, x_data.shape == (25, 1)

rand()

• 0과 1 사이 임의의 실수 값을 리턴해주는 함수
• 가중치(weight)나 바이어스(bias)를 임의로 설정할 때 자주 사용하는 함수

# 0 ~ 1 사이의 random number 발생

random_number1 = np.random.rand(3)
random_number2 = np.random.rand(1, 3)
random_number3 = np.random.rand(3, 1)

print("random_number1 == ", random_number1, ", random_number1.shape == ", random_number1.shape)
print("random_number2 == ", random_number2, ", random_number2.shape == ", random_number2.shape)
print("random_number3 == ", random_number3, ", random_number3.shape == ", random_number3.shape)

# 결과
random_number1 ==  [0.19724608 0.20855116 0.58046355] , random_number1.shape ==  (3,)
random_number2 ==  [[0.33375994 0.84088436 0.94006071]] , random_number2.shape ==  (1, 3)
random_number3 ==  [[0.8197173 ]
 [0.91239959]
 [0.30047281]] , random_number3.shape ==  (3, 1)

max(), min(), argmax(), argmin()

• max(), min() : 최대 최소를 리턴
• argmax(), argmin() : 최대 최소의 인덱스를 리턴

X = np.array([2, 4, 6, 8])

print("np.max(X) == ", np.max(X))
print("np.min(X) == ", np.min(X))
print("np.argmax(X) == ", np.argmax(X))
print("np.argmin(X) == ", np.argmin(X))

# 결과
np.max(X) ==  8
np.min(X) ==  2
np.argmax(X) ==  3
np.argmin(X) ==  0

X = np.array([[2, 4, 6], [1, 2, 3], [0, 5, 8]])

print("np.max(X) == ", np.max(X, axis = 0)) # 열 기준
print("np.min(X) == ", np.min(X, axis = 0)) # 열 기준

print("np.max(X) == ", np.max(X, axis = 1)) # 행 기준
print("np.min(X) == ", np.min(X, axis = 1)) # 행 기준

print("np.argmax(X) == ", np.argmax(X, axis = 0)) # 열 기준
print("np.argmin(X) == ", np.argmin(X, axis = 0)) # 열 기준

print("np.argmax(X) == ", np.argmax(X, axis = 1)) # 행 기준
print("np.argmin(X) == ", np.argmin(X, axis = 1)) # 행 기준

# 결과
np.max(X) ==  [2 5 8]
np.min(X) ==  [0 2 3]
np.max(X) ==  [6 3 8]
np.min(X) ==  [2 1 0]
np.argmax(X) ==  [0 2 2]
np.argmin(X) ==  [2 1 1]
np.argmax(X) ==  [2 2 2]
np.argmin(X) ==  [0 0 0]

ones(), zeros()

A = np.ones([3, 3])

print("A.shape == ", A.shape, ", A == ", A)

B = np.zeros([3, 2])

print("B.shape == ", B.shape, ", B == ", B)

# 결과
A.shape ==  (3, 3) , A ==  [[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]
B.shape ==  (3, 2) , B ==  [[0. 0.]
 [0. 0.]
 [0. 0.]]

matplotlib

• 실무에서는 머신러닝 코드를 구현하기 전에, 입력 데이터의 분포와 모양을 먼저 그래프로 그려보고, 데이터의 특성과 분포를 파악한 후, 어떤 알고리즘을 적용할 지 결정하고 있음
• 데이터 시각화를 위해 matplotlib 라이브러리를 사용함
• 일반적으로 line plot, scatter plot 등을 통해 데이터의 분포와 형태를 파악함

import matplotlib.pyplot as plt
import numpy as np

# 주피터 노트북을 사용하는 경우 노트북 내부에 그림 표시
%matplotlib inline

# x data, y data 생성
x_data = np.random.rand(100)
y_data = np.random.rand(100)

plt.title('scatter plot')
plt.grid()
plt.scatter(x_data, y_data, color = 'b', marker = 'o')
plt.show()

# x data, y data 생성
x_data = [x for x in range(-5, 5)]
y_data = [y*y for y in range(-5, 5)]

plt.title('line plot')
plt.grid()
plt.plot(x_data, y_data, color = 'b')
plt.show()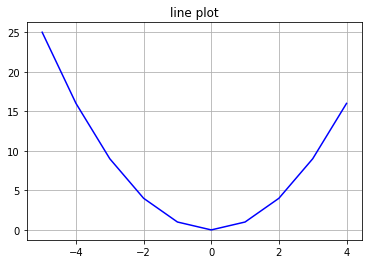

# x data, y data 생성
x_data = [-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
y_data = [-8, -13, 0, 3, 6, -1, -5, -7, 1, 8, 7, 12, 13]

plt.title('line plot')
plt.grid()
plt.plot(x_data, y_data, color = 'b')
plt.show()

 

 

 

참고

www.youtube.com/playlist?list=PLS8gIc2q83OjStGjdTF2LZtc0vefCAbnX

머신러닝/딥러닝 강의